Relative weight analyse: Welke aspecten van diensten en producten dragen het sterkste bij aan tevredenheid?
Key Drivers Analyse
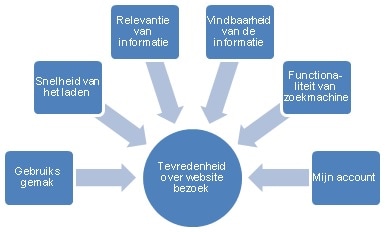
De vraag die in dit model centraal staat is de volgende: Welke van de diverse aspecten dragen het sterkste bij aan de hoogte van het algemeen oordeel? Hierbij ligt de focus op het verkrijgen van inzicht in het relatieve belang van de verschillende aspecten. Deze vraag wordt vaak beantwoord door middel van een zogenaamde Key Drivers Analyse.
In een Key Drivers Analyse wordt het relatieve belang meestal bepaald door middel van een multipele regressieanalyse, waarbij het algemeen oordeel (afhankelijke variabele) wordt geregresseerd op een reeks aspecten (de predictorvariabelen). Als maat voor het relatieve belang wordt dan gebruik gemaakt van partiële regressiecoëfficiënten.
Met deze aanpak wordt de centrale vraag echter niet beantwoord. Statistici hebben namelijk aangetoond dat, vooral in tevredenheidonderzoek, regressiecoëfficiënten in veel gevallen ongeschikt zijn voor het uitdrukken van het relatieve belang (Cohen, Cohen, West, & Aiken, 2003; Tonidandel & LeBreton, 2011). Een bekend probleem is namelijk het ontstaan van multicollineariteit; dat de predictorvariabelen onderling sterk correleren. Dit kan als gevolg hebben dat de coëfficiënten niet alleen een onjuist of onbetrouwbaar beeld geven, maar ook dat niet inzichtelijk kan worden gemaakt welke van de reeks aspecten de belangrijkste voorspellers van tevredenheid zijn. Wanneer bijvoorbeeld de twee aspecten ‘plezier en ‘uitdaging onderling sterk correleren (wie uitdaging in het werk ervaart, heeft vaak ook plezier in het werk) en beiden vertonen een substantiële samenhang met de algemene tevredenheid, dan zal een standaard regressieanalyse als uitkomst kunnen hebben dat een van de twee aspecten van belang is en de andere niet (meer). In veel gevallen overduidelijk een ongelukkige conclusie. De oplossing? Relative weight analyse.
Relative weight analyse
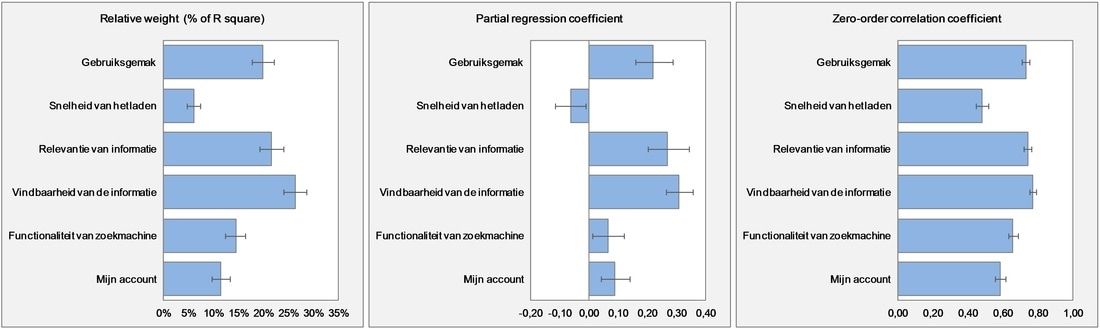
Relative weight analyse (Johnson, 2000; Tonidandel, LeBreton, & Johnson, 2009; Tonidandel & LeBreton, 2011) is een recentelijk ontwikkelde statistische procedure voor het betrouwbaar bepalen van het relatieve belang van een reeks predictorvariabelen in een regressiemodel. Het relatieve belang (of gewicht epsilon) is gedefinieerd als de proportionele bijdrage aan de verklaarde variantie die iedere predictor in het regressiemodel levert, waarbij zowel de unieke bijdrage van de predictor als de bijdrage in combinatie met andere predictoren wordt meegenomen. Relatieve gewichten zijn proporties met een waarde tussen de 0 en 1, waarbij de som gelijk is aan de totaal verklaarde variantie. Om de relatieve gewichten eenvoudig te kunnen interpreteren en inzichtelijk te rapporteren, kunnen deze worden omgezet naar percentages. Deze tellen op tot 100%, het totaal van de verklaarde variantie.
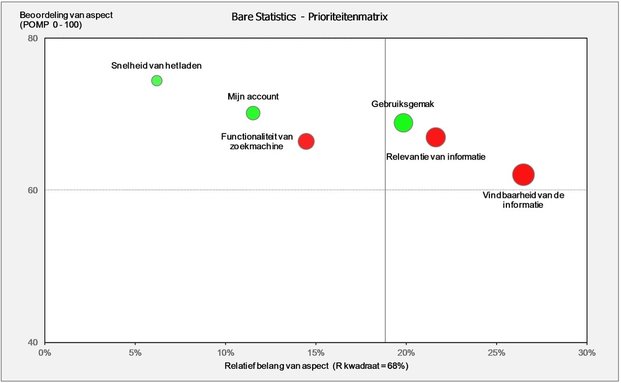
In een Key Drivers Analyse geven de relatieve gewichten een essentiële aanvulling op de uitkomsten van een regressieanalyse. Ze laten zien welke predictoren proportioneel de belangrijkste bijdrage geven aan de verklaarde variantie in het regressiemodel, en helpen dus de vraag te beantwoorden welke aspecten het grootste relatieve belang hebben. De uitkomsten van deze analyse laten zich eenvoudig interpreteren en lenen zich verder uitstekend als maat voor afgeleid belang in een prioriteitenmatrix.
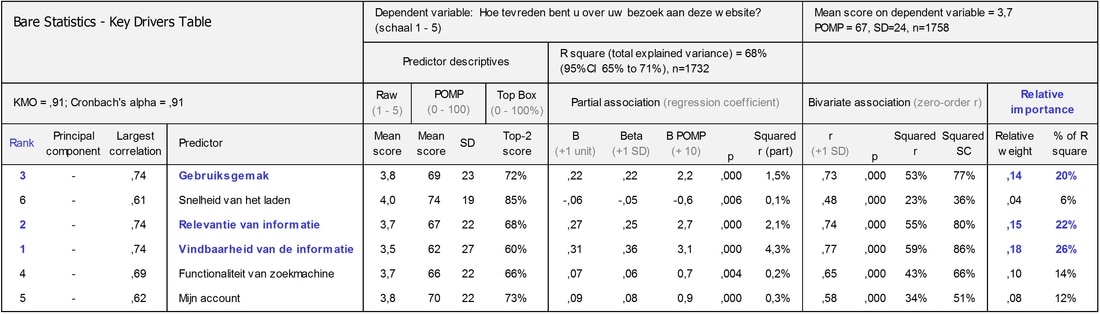
De uitkomsten van een Key Drivers Analyse laten zich het beste samenvatten in een gecombineerde tabel. Bare Statistics heeft hiervoor de Key Drivers Tabel ontwikkeld, waarin de resultaten van de corresponderende principale componentenanalyse, betrouwbaarheidsanalyse, beschrijvende statistieken, correlatieanalyse, multipele regressieanalyse en Relative weight analyse met elkaar kunnen worden vergeleken en in verband kunnen worden gebracht.
Op basis van een aangeleverd databestand kan Bare Statistics een Key Drivers Tabel produceren. Deze kan zeer snel en tegen een aantrekkelijk tarief worden geleverd.
Voor meer informatie, mail naar [email protected]
In een Key Drivers Analyse wordt het relatieve belang meestal bepaald door middel van een multipele regressieanalyse, waarbij het algemeen oordeel (afhankelijke variabele) wordt geregresseerd op een reeks aspecten (de predictorvariabelen). Als maat voor het relatieve belang wordt dan gebruik gemaakt van partiële regressiecoëfficiënten.
Met deze aanpak wordt de centrale vraag echter niet beantwoord. Statistici hebben namelijk aangetoond dat, vooral in tevredenheidonderzoek, regressiecoëfficiënten in veel gevallen ongeschikt zijn voor het uitdrukken van het relatieve belang (Cohen, Cohen, West, & Aiken, 2003; Tonidandel & LeBreton, 2011). Een bekend probleem is namelijk het ontstaan van multicollineariteit; dat de predictorvariabelen onderling sterk correleren. Dit kan als gevolg hebben dat de coëfficiënten niet alleen een onjuist of onbetrouwbaar beeld geven, maar ook dat niet inzichtelijk kan worden gemaakt welke van de reeks aspecten de belangrijkste voorspellers van tevredenheid zijn. Wanneer bijvoorbeeld de twee aspecten ‘plezier en ‘uitdaging onderling sterk correleren (wie uitdaging in het werk ervaart, heeft vaak ook plezier in het werk) en beiden vertonen een substantiële samenhang met de algemene tevredenheid, dan zal een standaard regressieanalyse als uitkomst kunnen hebben dat een van de twee aspecten van belang is en de andere niet (meer). In veel gevallen overduidelijk een ongelukkige conclusie. De oplossing? Relative weight analyse.
Relative weight analyse
Relative weight analyse (Johnson, 2000; Tonidandel, LeBreton, & Johnson, 2009; Tonidandel & LeBreton, 2011) is een recentelijk ontwikkelde statistische procedure voor het betrouwbaar bepalen van het relatieve belang van een reeks predictorvariabelen in een regressiemodel. Het relatieve belang (of gewicht epsilon) is gedefinieerd als de proportionele bijdrage aan de verklaarde variantie die iedere predictor in het regressiemodel levert, waarbij zowel de unieke bijdrage van de predictor als de bijdrage in combinatie met andere predictoren wordt meegenomen. Relatieve gewichten zijn proporties met een waarde tussen de 0 en 1, waarbij de som gelijk is aan de totaal verklaarde variantie. Om de relatieve gewichten eenvoudig te kunnen interpreteren en inzichtelijk te rapporteren, kunnen deze worden omgezet naar percentages. Deze tellen op tot 100%, het totaal van de verklaarde variantie.
In een Key Drivers Analyse geven de relatieve gewichten een essentiële aanvulling op de uitkomsten van een regressieanalyse. Ze laten zien welke predictoren proportioneel de belangrijkste bijdrage geven aan de verklaarde variantie in het regressiemodel, en helpen dus de vraag te beantwoorden welke aspecten het grootste relatieve belang hebben. De uitkomsten van deze analyse laten zich eenvoudig interpreteren en lenen zich verder uitstekend als maat voor afgeleid belang in een prioriteitenmatrix.
De uitkomsten van een Key Drivers Analyse laten zich het beste samenvatten in een gecombineerde tabel. Bare Statistics heeft hiervoor de Key Drivers Tabel ontwikkeld, waarin de resultaten van de corresponderende principale componentenanalyse, betrouwbaarheidsanalyse, beschrijvende statistieken, correlatieanalyse, multipele regressieanalyse en Relative weight analyse met elkaar kunnen worden vergeleken en in verband kunnen worden gebracht.
Op basis van een aangeleverd databestand kan Bare Statistics een Key Drivers Tabel produceren. Deze kan zeer snel en tegen een aantrekkelijk tarief worden geleverd.
Voor meer informatie, mail naar [email protected]